Présentation générale
Les roues codeuses sont un élément vital du robot. Elles permettent de contrôler ses déplacements. D’une manière générale, ces pièces sont particulièrement coûteuses. Nous allons essayer d’en réaliser à moindre coût.
La fonction d’une roue codeuse est de renvoyer un signal qui dépend du déplacement effectué par la roue. Les roues codeuses industrielles sont généralement composées d’un faiseau lumineux et d’une roue perforée de manière régulière. Suivant la position de la roue, le faisceau lumineux est interrompu ou non. Un capteur détecte la présence du faisceau et renvoie un signal électrique. Plus la roue tournera vite et plus les créneaux du signal seront rapprochés.
Nous allons utliser le même principe, à partir de fourches infrarouges et d’un disque imprimé sur du papier transparent. Notre robot dispose de deux roues porteuses qui sont des roues de roller. Ce sont sur ces roues que nous allons fixer les codeurs. Pour espacer le disque de la roue, nous réalisons une sorte d’entretoise en carton ondulé.
Réalisation
Pour les fourches infrarouges (ref TCST1103 chez farnell), nous comptons les fixer sur un support en bois. A cause de l’épaisseur du faisseau (environ 1mm), nous sommes obligés d’avoir une zone opaque supérieure à 1 mm en bout de roue.
Nous réalisons une roue de 5cm de diamètre avec 60 bandes noires alternées avec des zones transparantes. La roue est dessinée avec Inkscape. L’impression des dessins à la bonne taille se fait en exportant le fichier en eps (qui est un format vectoriel) pour l’importer dans un traitement de texte. Il sera possible ici de définir une taille du dessin en centimètres. Attention, ça peut baver un peu à la sortie de l’imprimante.
Un premier essai nous montre que notre entretoise était trop large. Nous décidons de réduire le diamètre extèrieur à 3 cm pour laisser 1 cm de pénétration au capteur.
Le disque imprimé s’abîme très vite, l’encre se détache facilement du disque, surtout en cas de frottement. Nous prévoyons de coller un disque transparent du côté de l’encre afin de préserver le disque.
Capteurs
Nous commençons ensuite la partie capteur. Première question que nous pourrions nous poser : Pourquoi mettre deux fourches par roues ?
Avec deux signaux correctement déphasés, il est possible de connaître le sens de rotation de la roue et ça, c’est particulièrement intéressant si nous souhaitons faire tourner le robot sur lui-même. Car dans ce cas, une roue avance et l’autre recule.
Le déphasage, c’est quoi ?
Le déphasage est un décalage temporel entre deux signaux identiques. La différence entre un retard et un déphasage est assez mince. Dans notre cas, nous retiendrons que si un retard est exprimé en unité de temps (généralement en secondes), ce n’est pas le cas du déphasage. Le déphasage est un retard qui dépend de la période du signal. Il est généralement exprimé en unité d’angle (en degrés ou en radian).
Par exemple :
- Deux signaux qui ne présentent aucun retard auront un déphasage de 0 (degrés ou radians).
- Deux signaux qui présentent un retard d’une période complète auront un déphasage de 2.PI ou 360°.
- Des signaux qui sont légèrement décalés comme ceux ci-dessous ont un déphasage de 15° (ou 0,26 radian).
Comment se crée le déphasage dans notre cas ?
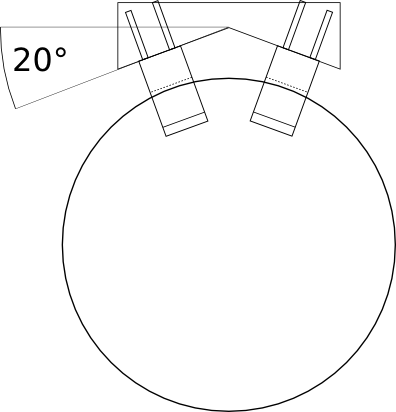
Dans notre cas, le déphasage se crée en positionnant correctement les capteurs. Comme on peut le voir sur le schéma suivant, en position initiale, les deux capteurs voient le faisceau lumineux. Si la roue tourne dans le sens 1, on s’aperçoit que le faisceau du capteur 1 sera interromptu avant celui de capteur 2. Si la roue tourne dans l’autre sens, c’est le faisceau du capteur C2 qui sera coupé en premier.
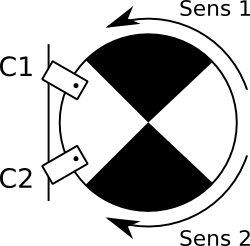
Les capteurs C1 et C2 sont nos fourches infrarouges.
On comprend l’interêt du déphasage en mémorisant la valeur d’un signal lors du front montant de l’autre signal.
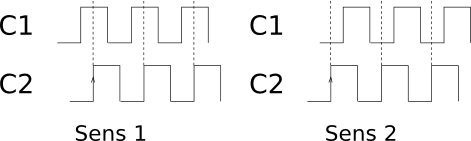
Nous avons maintenant notre moyen de connaître le sens de rotation de notre roue.
Principale difficulté
Notre problème vient du centrage du disque codeur par rapport à la roue. Si le disque est mal centré, le capteur ne sera pas à une distance constante du centre de la roue codeuse. Ceci est problématique car le déphasage dépend de cette distance. Nous voulons calculer l’impact qu’aurait un décentrage sur le déphasage pour être sûr que celui-ci reste acceptable.
Le déphasage idéal est de 90°, un quart de période. Les valeurs extrêmes à ne pas atteindre sont 0° (les deux signaux sont superposés ou en phase) et 180° (les signaux sont à l’opposé l’un de l’autre, dits en opposition de phase). Dans ces deux cas si la roue change de direction nous ne pouvons pas le détecter. Pire, si la valeur du déphasage oscille autour de l’une de ces deux valeurs, nous auront l’impression que la roue change de sens alors que ce n’est pas le cas.
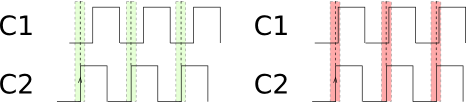
Dans le cas de gauche, sur l’image ci-dessus, le déphasage vaut un quart de periode. Si le déphasage varie un peu (dans la zone verte), notre lecture du sens de rotation restera bonne. Par contre, dans le cas de droite, où la valeur du déphasage est proche d’une période ou d’une demi-période, même une légère variation du déphasage peut entraîner une erreur de lecture du sens de rotation de la roue.
Notre roue compte 60 bandes opaques alternées avec 60 bandes transparentes. Notre période angulaire est d’un soixantième de tour, soit 6 degrés. Pour avoir un déphasage d’un quart de période, il faut donc espacer les capteurs de 1,5 degrés sur la roue. Ceci nous obligerait à avoir des capteurs particulièrements proches (ou à avoir une roue particulièrement grande). Nous allons alors rajouter un nombre entier de période pour les espacer. Ça, c’est encore de la théorie. Dans la pratique, l’espacement entre nos deux capteurs est fixe et il faut ajuster la distance entre les capteurs et le centre de la roue pour obtenir le déphasage idéal.
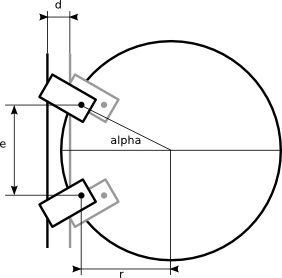
La variation de d, influe sur l’angle alpha qui nous permet de déterminer le déphasage. alpha = arc_tan(e/2r). En rajoutant la variation d, on a alpha = arc_tan(e /(2r+2d))
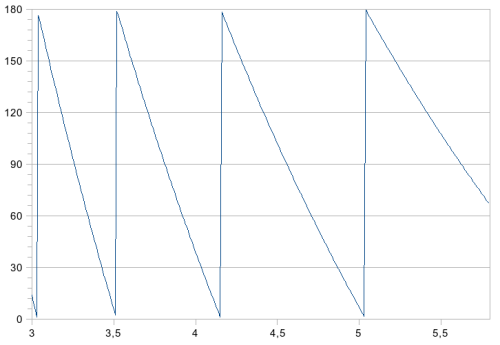
Le graphique suivant donne le déphasage que l’on observerait en fonction de la distance des capteurs par rapport au centre de la roue. La valeur du déphase est remise à 0 toutes les demi-périodes (180°). Ceci permet de mettre en évidence les zones à éviter. L’écartement entre les deux capteurs (2,7 cm) a été choisi de manière à se retrouver dans un cas favorable. Ici, les capteurs peuvent bouger de huit millimètres (entre 4,2 cm et 5 cm) par rapport au centre de la roue sans que nous ayons de problèmes avec la phase.
