Les robots autonomes embarquent dans leurs circuits électroniques une puissance de calcul permettant à la fois de piloter la trajectoire du robot et de l’exécuter en contrôlant les consignes d’asservissement nécessaires.
Mais on peut très bien développer une intelligence artificielle embarqué en conservant un contrôle sur le robot. Il n’est plus autonome au sens robotique du terme, puisque nous allons le télécommander, mais il reste suffisamment à faire sur les algorithmes de calculs des consignes moteurs pour ne pas se compliquer la tâche.
On va présenter ici une interface de contrôle, composée d’une IHM (un écran graphique de commande du robot, permettant d’afficher les différentes valeurs numériques, consignes ou variables télémétriques, et d’une interface matérielle de communication avec le robot.
La télécommande choisie permettra de donner au robot une vitesse moyenne et un biais (angle d’écart) qui fera pivoter le robot. On appelle ce contrôle "polaire" par opposition au contrôle "cartésien" qui utilise comme consignes les coordonnées x et y d’un point à atteindre.
De manière générale, les coordonnées polaires sont le rayon (distance entre le point concerné et le centre) et l’angle (valeur trigonométrique de l’angle entre une origine et le rayon). En robotique, l’origine est généralement donnée par la direction du robot.
Interface graphique
Voici l’application réalisée (sous Processing) :
On utilise les flèches du clavier pour changer les valeurs polaires, ou le pavé numérique pour changer les valeurs cartésiennes. L’interface peut également suivre le curseur de la souris (un clic pour activer, un autre clic pour désactiver) mais à terme, on remplacera la souris et le clavier par un joystick ou une manette WII.
Note : le radar utilisé pour l’interface graphique est un écran du Royal Air Force Air Defence Radar Museum (Royal Air Force Neatishead, Near Horning, Norfolk, England, UK ) et la photo est issue d’un album de Leo Reynolds sous licence Creative Commons.
Polaire à cartésien
C’est le sens le plus simple :
– x = rayon * cosinus (angle)
– y = rayon * sinus (angle)
Cartésien à polaire
Plus délicat pour l’angle, car il faut discriminer les différences de signe entre x et y car on utilise le rapport y/x (x doit donc être non nul) et la fonction arctangente. La comparaison du signe de x et du signe de y s’apparente à indiquer dans quel "quadrant" du cercle on se trouve.
Au final, cela donne :
– rayon = racine carrée de x puissance 2 + y puissance 2
– angle = arctangente du rapport y sur x + ou - 360 degrés
En langage de programmation, c’est plus simple car généralement on dispose de deux fonctions arctangente : atan2 prend en argument le x et le y et s’occupe de discriminer les différents cas, ce qui donne :
– r = sqrt(pow(x,2)+pow(y,2) où sqrt() est la fonction racine carrée et pow() la fonction générique "puissance"
– theta = atan2(x,y)
Consignes de vitesse
Notre but étant de piloter un robot à distance, nous n’allons pas faire d’asservissement polaire pour l’instant, on va considérer que le rayon représente la vitesse moyenne et l’angle un biais qui donne une orientation à gauche ou à droite plus ou moins forte. Ce qui donne très simplement :
– vitesse gauche = rayon - angle
– vitesse droite = rayon + angle
Vérification : si la vitesse moyenne / rayon vaut 50 et que l’angle est de 25, cela donne une vitesse sur le moteur gauche à 25 et une vitesse sur le moteur droit à 75. C’est logique car 25 est un angle positif, donc demandant de tourner à gauche, donc d’avoir une vitesse à droite plus grande.
Si vous avez un meilleur algorithme, contactez-moi car je cherche à prendre en compte le fait qu’un angle de 90° devrait donner une rotation sur place plus ou moins forte. Mais nos tests sur l’interface de pilotage montre une cohérence même dans les quadrants arrières (rotation du robot pour retourner en arrière).
Nouvelle version
Pour ceux qui veulent essayer, voici un patch pour Pd qui fait la même chose (avec des sliders) :
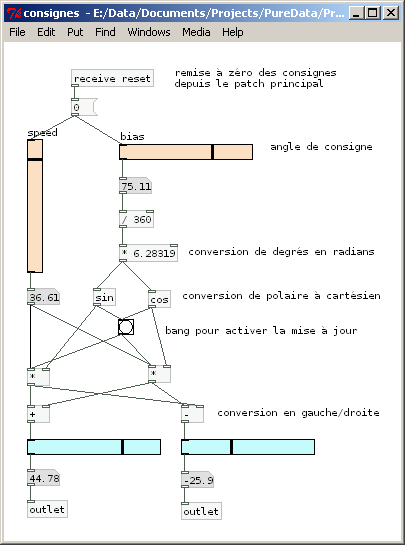
Il s’agit d’un sous-patch du projet "demo-odométrie" que vous trouverez sur le Playground avec tous nos autres projets (dans la catégorie Pure Data bien sûr). Lien ci-contre pour tous nos codes sources.
 PoBot
PoBot
 Télécommande en contrôle polaire
Télécommande en contrôle polaire



