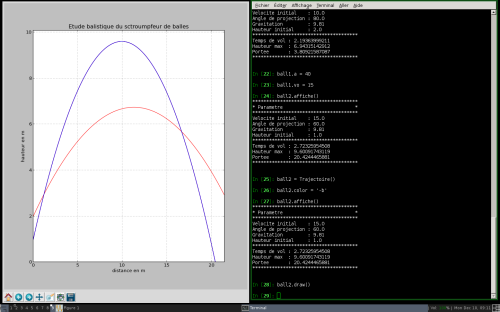
Voici une petite classe que j’avais faite lorsque j’ai commencé à travailler sur des lanceurs de balles.
Le but était de me familiariser un peu avec la balistique et Matplotlib.
Si vous voulez juste un résultat rapide, cette application en ligne répondra bien mieux à vos attentes.
Le script était cassé par le passage à python3 et la refonte de ipython. Mais c’est réparé ! L’exemple est minimal et je ne le considère pas comme terminé, mais je trouve qu’il a son intérêt dans le contexte.
La balistique est un problème assez récurrent en robotique, les lycéens retrouverons un sujet étudié en cours, et Matplotlib pourrait s’avérer être une alternative séduisante à Matlab [1] :
- libre
- puissante grâce à python et ses modules
- interactive avec Ipython
Le but ici n’est pas de réécrire la doc de matplotlib, de Numpy et encore moins de python... (et non il faudrait d’abord que je les lise :) ) mais je vous mets quelques liens bien choisis que vous n’auriez je suis sûr jamais trouvé tout seul :) :
- ipython :
- matplotlib :
- numpy :
- balistique :
- python :
- le décorateur property (je connais ça depuis pas longtemps, c’est bien pythonique) :
Contenu de la classe
Voici le script .py à télécharger :
On commence par importer les ressources python utiles :
import numpy as np
import matplotlib.pyplot as plt
import IPython
from pylab import ion
Et on complète la classe avec les formules mathématiques :
def x_max(self) :
vo, a, g , yo = self.vo , self._a, self.g, self.yo
x_max = ( vo**2. * np.sin(2.*a) ) / (2.*g) \
+ np.sqrt( ( (vo**2. * np.sin(2.*a))**2. ) / (4.*g**2.) \
+ ( 2.* yo * (vo * np.cos(a))**2.) / g )
return x_max
def y_max(self) :
vo, a, g , yo = self.vo , self._a, self.g, self.yo
y_max = ( vo**2 * np.sin(a)**2 ) / ( 2*g ) + yo
return y_max
def temps_de_vol(self) :
vo, a, g , yo = self.vo , self._a, self.g, self.yo
temps_total = ((vo * np.sin(a) ) / g ) + ( np.sqrt( (vo*np.sin(a))**2 + 2*g* yo) / g )
return temps_total
def equation(self, x) :
vo, a, g , yo = self.vo , self._a, self.g, self.yo
y = -( g / ( 2 * (vo * np.cos(a))**2) ) * x**2 + np.tan(a) * x + yo
return y
def config_axes_equation(self) :
size_x_max = self.x_max() + 5./100. * self.x_max()
size_y_max = self.y_max() + 5./100. * self.y_max()
return (size_x_max, size_y_max)
def matrix_equation(self, precision = 0.1) :
x = np.arange( 0.0, self.x_max(), precision )
y = self.equation(x)
return (x, y)
Exemple d’utilisation
– vo = vitesse initial en m/s
– a = Angle de tir en degrés
– yo = Hauteur initial de tir en m
$ python balistik.py
In [1]: ball1 = Trajectoire(vo=10, a=80, yo=2)
In [2]: ball1.affiche()
In [3]: ball1.a = 40
In [4]: ball1.vo = 15
In [5]: ball1.affiche()
In [6]: ball1.draw()
In [7]: ball2 = Trajectoire()
In [8]: ball2.draw() PoBot
PoBot