- Je rédige cet article pour partager les recherches que j’ai effectué dans le cadre du TIPE en 2ème année de classe prépa.
- Le but est d’établir puis de comparer les différentes façons d’obtenir le champ électromagnétique dans des éléments simples (bobine, aimant, électroaimants).
I bobine et magnétisme
a) la théorie avant tout
- Le plus évident lorsque l’on veut la norme du champ magnétique en certains points (et non plus uniquement le sens) est de passer par la théorie.
Pour cela, on se place sur l’axe central et on se sert de la formule du solénoïde à n spires :
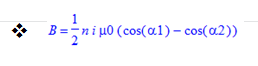
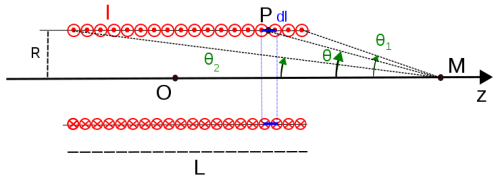
où uo est la perméabilité du vide (4π×10-7 H/m).
où n est le nombre de spires par mètre ( n= N/L , N : nombre total de spires de la bobine, L:longueur de la bobine).
où I est l’intensité (paramètre que l’on peut donc faire varier).
où cos alpha1 ou 2= c.adj / hypoténuse (prendre le contour de la bobine, et utiliser une simple règle) (paramètre que l’on peut faire varier pour avoir le champ à une distance précise sous la bobine).
- A l’aide d’excel, il suffit ensuite de modifier les variables i ou cos teta 1 et 2 pour avoir tous les champs possibles en fonction de l’intensité et de la distance.
Pour exemple : http://www.pobot.org/IMG/png/excel.png
b) Et en vrai, on obtient quoi ?
La pratique n’est pas vraiment similaire à la théorie. Cherchons l’écart entre les deux.
- On se sert d’un teslamètre, c’est à dire d’un appareil qui permet de mesurer le champ magnétique en mTesla. On le place à la distance voulue sous la bobine (alimentée par le courant souhaité), et on relève simplement le champ électromagnétique à chaque mesure..
NB : Le protocole pour l’utilisation du teslamètre sera détaillé plus loin.
- Voilà une idée, après relevé des mesures et passage par excel de ce que l’on peut obtenir lorsqu’on trace les courbes théoriques et experimentales :
Les chiffres apres les noms indiquent le courant. Pour comprendre : le nom « exp1 » signifie « courbe du relevé expérimental effectué à 100mA » .
Analyse du graphique :
– La formule théorique se rapproche de très près à la pratique (de l’ordre du demi mT de différence).
– Outre une erreur quand le capteur hall (du teslamètre) est trop proche de la bobine, on constate que la valeur réelle du champ B est légèrement inférieure à la théorie, ce qui est cohérent au vu des pertes et des perturbations.
II aimant et magnétisme

- On s’intéresse à un aimant néodyme de 8mm de diamètre sur 1mm d’épaisseur.
Les aimants ne figurant pas au programme de prépa, la formule pour le calcul de champ sur un aimant (si elle existe) m’était inconnue. Je ne l’ai donc pas utilisée.
a) Mesure « à la main » du champ électromagnétique
- J’ai décidé d’obtenir une carte de champ complète sous l’aimant dans un volume de 10cm carré sur 3 de profondeur. Soit 300 mesures si on espace les mesure chacune d’un cm carré. Il faut donc être patient.
- Rien de plus facile ensuite : le teslamètre est là pour nous servir !
Attention : le teslamètre scolaire que j’ai utilisé permet de mettre en évidence des champs importants (pour palier au champ terrestre et être sur que les élèves voient quelques chose). Les champs étant ici faibles, la manipulation devient beaucoup plus délicate !! Les données seules de l’axe vertical du teslamètre m’ont servie.
.

Voici le teslamètre. Attention, il se dérègle très rapidement à cause de toutes les perturbations (notamment terrestre).

- Chaque intersection de la grille correspond à une mesure. Il suffit donc de déplacer l’extrémité du capteur à l’endroit voulu 100 fois puis de descendre le support élévateur d’un cm et de recommencer. Un double de la grille permettait de noter les mesures.
De façon générale, éviter toute partie métallique parasite à moins de 10cm du teslamètre ! Par ex : les vis, la tige en métal, des pinces crocos pour tenir l’aimant etc. D’où le polystyrène et le rouleau en carton pour tenir l’aimant.
Surtout, ne jamais déplacer le teslamètre ni l’éteindre une fois taré... vous êtes bon pour recommencer un autre jour !
b) modélisation 3D
- Une fois les mesures effectuées, comment les rendre exploitables ?
On a 300 données en milliTesla (mT) chacune disposée à un endroit géographique précis. Et bien trouvons un logiciel capable de dessiner les 300 vecteurs B à leurs place respectives !
- La solution trouvée : la version Beta de geogebra 5 qui propose un tableur 3D !!
- Il suffit de rentrer pour chaque vecteur : le point de départ (x,y,z), le point d’arrivée (x,y,z), puis de demander de tracer une flèche entre les 2 points.
Soit 900 points et 300 flèches. Avec un peu d’astuce il en reste finalement peu à rentrer (c’est un tableur !)
- Ça donne quelque chose du genre (juste un petit bout, le tableur est bien plus grand en fait) :
http://www.pobot.org/IMG/png/geo.png
- C’est illisible ! Il y en a trop. Si on garde juste la pointe du vecteur on obtient :
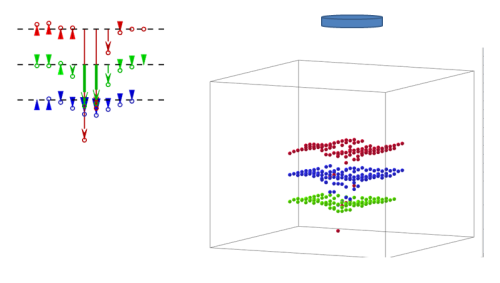
- Analyse :
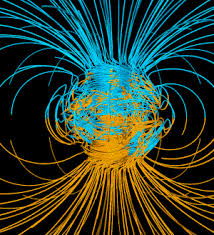
– On retrouve tout d’abord dans les mesures le sens des lignes de champ (négatif à droite, positif à gauche).
– Le champ est aussi plus fort sous l’aimant, ce qui est cohérent.
– Grace au nuage de points qu’on a crée, les lignes de champs apparaissent clairement, ce qui était initialement recherché !
III Modélisation logicielle
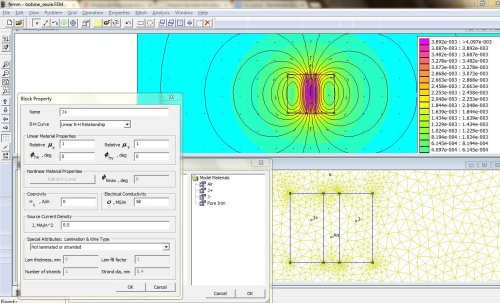
- J’ai découvert un logiciel que je souhaite vous faire découvrir, qui permet de faire çà :
- Ce logiciel s’appelle FEMM (Finite Element Method Magnetics). Il permet de modéliser des pièces et d’en faire apparaître les champ magnétiques ou électrostatiques selon leurs dimension, et leurs compositions.
- Procédons sous la forme d’un mini tuto.
– Télécharger femm
– Voici le tuto proposé via ce lien]
– Il sera plus complet que tout ce que je pourrais dire.
Quelques commentaires :
– C’est en anglais, mais la physique, c’est partout pareil ! Les seules difficultés seront de trouver le bon matériau (iron, magnet, steel, copper, coil... m’enfin).
– Femm offre alors de modéliser un objet en 2D puis, soit de lui donner une profondeur (type pavé), soit de l’arrondir (type cylindre, sphère...).
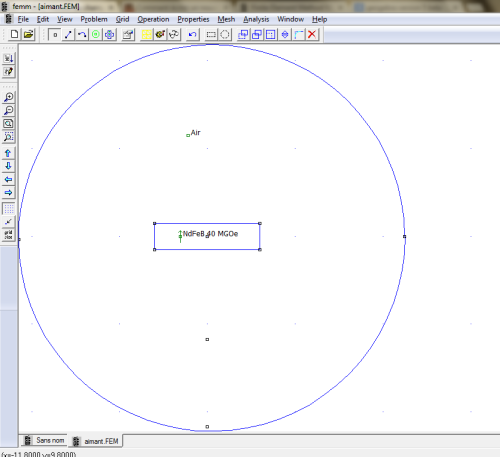
- Çà, c’est mon aimant cylindrique, aux bonnes dimensions.
– a)Pour faire un cercle : tracer 2 points, puis un arc de cercle entre les 2. Le logiciel ne trace que des morceaux de cercle. L’angle max est donc de 180 degrés. Le demi-cercle ira du premier point au 2ème sélectionné. Pour fermer le cercle, il suffit donc de refaire un demi cercle de 180° allant du 2ème au 1er.
– b)Pour faire un rectangle : placer les points des coins puis les relier avec des traits. Attention : Il n’y a pas de placement automatiques, faites en sorte d’avoir assez zoomé pour placer le point correctement. Sinon, ses coordonnées seront par ex (3,02 ;0,06) et non pas (3 ;0). Il en va de même pour les cercles (un diamètre de 21mm, c’est pas un diamètre de 20mm...).
– Je suggère, n’ayant pas tout saisi, de bien suivre le tuto pour les rentrées de données un peu compliquées. A moins de les connaitre.
– Ici, par exemple, la densité de courant, c’est simplement le courant (de 500mA).
ux et uy à 1 : pas de perméabilité. J+, en opposition à J- : noms que j’ai donné à 2 parties de la bobine pour orienter le sens du courant.
- Ensuite, il suffit de définir un périmètre de calcul (une condition aux limites) puis d’appuyer sur 3 boutons à la suite :

triangulation,calcul, affichage
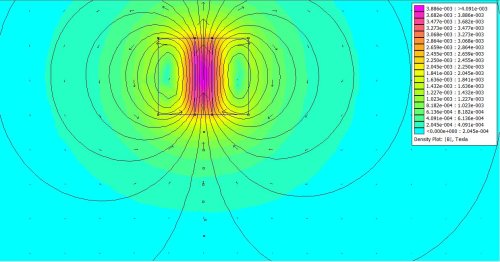
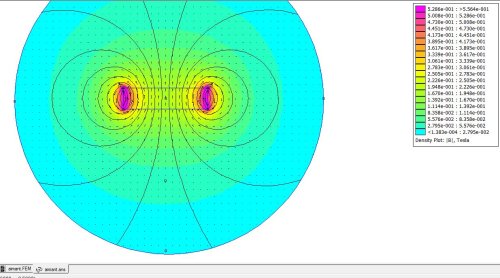
- A titre d’exemple, cela donne pour notre aimant :
- A 1cm sous l’aimant, on mesure 20mT, contre 10mT dans la réalité, ce qui est plutôt pas mal !
- Encore à titre d’exemple, voilà ce que l’on obtient avec un électroaimant constitué d’un fer doux un peu spécial. Les données en gras sont celle mesurées sur le vrai électroaimant pour un courant de 500mA.
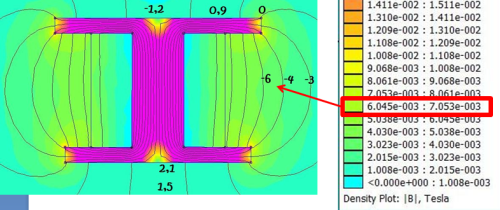
C’est encore plus cohérent !
Attention : étonnement, la démarche n’a pas marché avec le solénoïde fini seul. J’ai surement omis de rentrer une donnée qui empêche le résultat d’être cohérent avec ce qui a été mesuré au grand I de cet article. N’étant pas maître du logiciel femm, peut être (je ne crois pas) est-ce de la chance qui m’a permis de trouver de bon résultats pour les électroaimants.
conclusion
- A terme, outre d’approfondir mes connaissance de l’électromagnétisme, le but était de pouvoir disposer de moyens me permettant d’obtenir par moi-même les propriétés physiques de composants électroniques tels que les bobines et les électroaimants. Et surtout, de pouvoir en vérifier la véracité et la précision !
- Les valeurs mesurées par les différents mode de calculs n’ayant jamais été identiques, il m’est impossible de dire quel moyen est le plus précis. Sans doute une moyenne des 3 (ou 4) moyens identifiés permettrait d’avoir un bon ordre d’idée.
Elargissement :
– Il est entendu que de la simple poussière métallique, ou une boussole permettent rapidement l’obtention des lignes de champ. Le ferrofluide ainsi que certaines feuilles « poudrées » permettent aussi d’avoir proprement les lignes de champ !
– Par chance, le logiciel femm peut aussi nous donner l’inductance de ces matériau s’ils sont correctement modélisés. Ce qui offre encore plus de possibilités d’étude !
Les propriétés de ce logiciel sont encore bien inexplorées et les tutoriels absents de la toile française.
 PoBot
PoBot
 Mesure du champ électromagnétique
Mesure du champ électromagnétique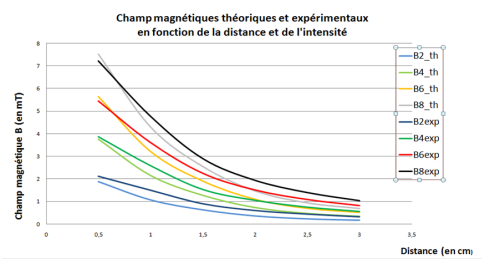







Vos commentaires
# Le 14 décembre 2020 à 09:42, par Magnon 86 En réponse à : Mesure du champ électromagnétique
En réponse à : Mesure du champ électromagnétique
Merci pour le fruit de votre travail.
Cela permet d avoir à disposition de tous une idée d’application des connaissances théoriques sur le magnétisme, et surtout des logiciels et instruments de mesure pour vérifier ce que l’on croyait savoir (dans l’esprit de Descartes et de l’ingénierie moderne).
C’est donc en ancien ingenieur que je dis que c’est avec mérite que votre page se trouve dans les premières dans les outils de recherche, sans qu’on ait besoin de passer par les géants américains (avec leurs qualités encyclopédiques et leurs défauts hégémoniques).
Répondre à ce message
# Le 5 février 2017 à 19:18, par LERMYTTE En réponse à : Mesure du champ électromagnétique
En réponse à : Mesure du champ électromagnétique
Bonjour, je me suis moi même lancé dans la mesure du champ magnétique d’un aimant. J’ai effectué plus de 300 mesures également. J’aimerais comprendre ce que représente vos "points de départ" et vos "points d’arrivés lors de la création du graphique. Merci beaucoup
Répondre à ce message