Intérêt du robot rond

Le robot est un modèle à roues différentielles (type char), doté d’un châssis circulaire de 100 mm de diamètre. Le choix de la géométrie est dicté par la symétrie centrale du disque. En effet lors de la détection d’un obstacle par les capteurs IR de proximité, le châssis circulaire garantit un dégagement par inversion du sens de rotation des roues (en tournant sur place). Lors de cette rotation on peut être certain que si l’avant du robot n’était pas au contact de l’obstacle au moment de la détection, aucune partie du châssis ne touchera l’obstacle durant le dégagement. Par opposition, les châssis rectangulaires impliquent une logique de dégagement nettement plus complexe pour garantir que les bords ou l’arrière du robot ne viendront pas frotter l’obstacle au cours du mouvement.

Rappelons que si le châssis du robot frotte sur un obstacle, il va en découler un probable dérapage d’une des roues et donc une perte de position pour le programme de guidage. La roue tournant, les capteurs odométriques continuent à informer la CPU d’un déplacement qui ne se réalise pas réellement. Au sortir de cette collision l’algorithme de positionnement travaille alors avec un cap et une position erronés.

La question des roues

Un autre élément de géométrie très important, concerne l’épaisseur des roues. Pour réaliser des asservissements en position et/ou vitesse il est primordial d’avoir un « modèle géométrique » du robot le plus précis possible. Par « modèle géométrique » il faut entendre : connaître avec précision le diamètre des roues et la distance séparant ces deux roues. Les capteurs odométriques mesurent le déplacement des roues en nombre de tours, de dixièmes, ou de centièmes de tours pour savoir quand arrêter le mouvement ....

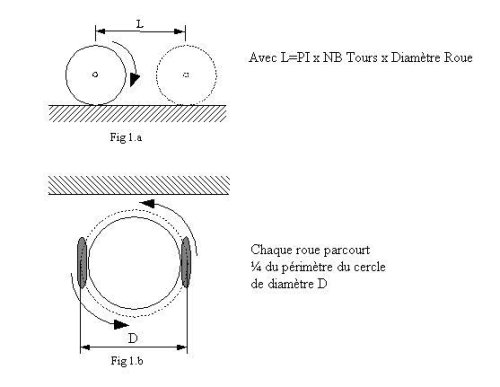
 le diamètre des roues car on ne mesure pas directement la distance parcourue par la roue mais le nombre de tours qu’elle fait. Par conséquent pour connaître la distance parcourue lors d’un tour, il nous faut calculer Pi x diamètre de la roue x nombre de tours. (Figure 1a)

 l’écartement entre les roues : imaginez que vous vouliez que votre robot fasse un quart de tour sur place : il faut que chacune des roues parcourt, en sens opposé, le périmètre d’un quart de cercle - cercle dont le diamètre correspond à l’écartement des deux roues. (Figure 1b).

Avec des roues larges il est impossible de déterminer en permanence où se situe le point de contact roue/sol : est-ce le milieu de la roue, le bord intérieur, le bord extérieur ? Les roues les plus étroites possibles n’offrent, elles, aucune ambiguïté le point de contact. Le « modèle géométrique » (diamètre des roues, écartement des roues) est alors très bien connu.

Précédent : introduction

Suivant : construction des éléments