Traitement d’image

Petite mise en bouche

Comme rapidement présenté dans l’article sur la valise TaxiBot, le traitement d’image permettant la génération du programme des déplacements du robot à partir des cartes disposées sur le plateau est basé sur OpenCV et son binding pour Python.

Au coeur de processus se trouve la phase d’identification de chacun des symboles présents sur le plateau, sur la base de leur image de référence.

Analyse du problème

Nous sommes dans un contexte relativement fini, à la différence d’un système embarqué dans une voiture devant reconnaître les panneaux de signalisation qui défilent. Par ailleurs les symboles à reconnaître sont en noir et blanc. Nous pouvons donc simplifier le problème et éviter de devoir recourir à une artillerie lourde du genre machine learning et autre technologies très hype actuellement. Nous aurions pu le faire histoire de se la péter, mais il n’y avait aucune réelle valeur ajoutée et uniquement des risques de dysfonctionnement en cas de maîtrise imparfaite de ces outils.

L’approche retenue, relativement simple dans son principe, est de chercher à superposer l’image théorique (c’est à dire issue de leur dessin vectoriel) des symboles à reconnaître aux emplacements auxquels ils sont supposés apparaître, c’est à dire dans les cases de la grille du plateau.

Remarque : le point n’est pas utilisé pour programmer les déplacements du robot et a une utilisation spécifique que nous verrons un peu plus loin.

On mesure ensuite le taux de correspondance entre la partie de l’image capturée et l’image modèle du symbole, et on décide en fonction de la valeur si le symbole essayé est celui qui est à l’emplacement analysé... ou pas.

La théorie est très simple, mais la réalité est un peu plus délicate, car nous allons appliquer cette méthode à une photo qui est tout sauf une image parfaite.

Bienvenue par conséquent dans la fabuleuse aventure de l’analyse d’image et suivons pas à pas ce qui se passe en coulisse.

Point de départ

Voici un exemple d’image telle que capturée par la caméra :

C’est une image en couleur, et on constate immédiatement que :

• bien que le sujet photographié soit principalement des symboles noirs sur un fond blanc, l’image présente une teinte un peu rosée, causée ici par l’éclairage ambiant
• elle est de travers et légèrement déformée (en caramel)
• on y voit d’autres choses que nos symboles et notamment une partie de l’intérieur de la valise sur la gauche

Rappelons-nous que l’objectif est d’identifier des symboles spécifiques dans une zone rectangulaire quadrillée en 4 lignes de 5 colonnes.

Nous, les humains, sommes capables d’analyser l’image de manière globale et d’y reconnaître des choses instantanément. Ce qui permet ce prodige est l’incroyable capacité du cerveau à traiter un grand volume d’information en parallèle, même si nous n’en avons pas conscience et également à fonctionner par association.

La machine va procéder de manière beaucoup plus primaire et rechercher les correspondances entre symboles de référence et portions d’image par superposition. Dit plus simplement, on place le symbole à un endroit où on pense pouvoir le trouver (comme s’il était dessiné sur du papier calque) et on regarde si ça correspond.

Pour faire cela, il va falloir repérer dans un premier temps les zones d’intérêt, c’est à dire celles où les symboles peuvent se trouver. A la base il s’agit des cases de la grille. Mais comme le montre l’image brute, elles ne sont pas à des positions bien définies, ces positions peuvent varier selon la prise de vue et la manière dont le plateau a été posé et enfin elles sont un peu déformées.

La première chose à faire est donc de transformer l’image de manière à en extraire la zone à analyser et à lui restituer des caractéristiques géométriques connues, c’est à dire un quadrillage régulier et dont les axes sont orthogonaux. Cela s’appelle le recadrage ou recalage.

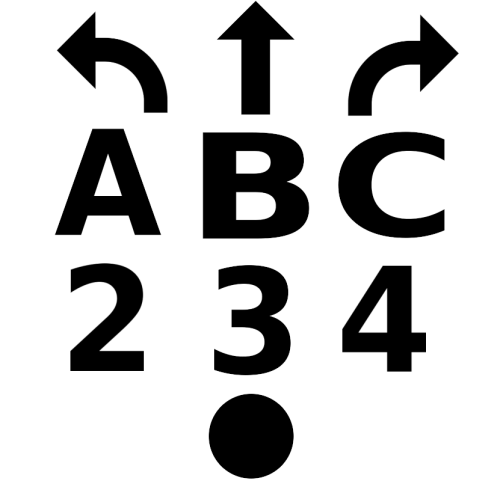
Nous allons pour cela nous aider des quatre repères en forme de gros points noirs qui l’encadrent, et c’est donc ce symbole qui va être recherché en premier.

Le choix d’un point et non pas d’une croix ou autre graphisme n’est pas dû au hasard, mais parce que notre point est géométriquement parlant un disque et est donc invariant par rotation. En termes moins barbares, il ne change pas de forme quel que soit l’angle dont on le fait tourner, autrement dit, dans n’importe quelle position. Cela rend de fait plus simple la recherche de correspondance, en éliminant l’influence de la rotation du motif.

Simplification de l’image

Une photo représente une gros volume de données, car chaque pixel encode la couleur, en général sous forme de ses 3 composantes primaires rouge, vert et bleu (codage RGB, ou RVB en Français) comme le font des caméras telles que celle qui est utilisée ici. Chacune de ces composantes est codifiée sous forme d’un octet valant entre 0 et 255 et représentant son intensité dans le mélange que constitue la teinte restituée, ce qui occupe donc 3 octets par pixel. A noter que d’autres codages de la couleur existent, comme le HSL ou HSV, mais ils utilisent tous le même nombre de composantes.

Plus le volume de données est conséquent et plus le temps de traitement le sera. Il est donc très rentable de chercher à le réduire, tout en ne perdant pas d’information indispensable au traitement. Dans notre cas de figure, la couleur n’apporte pas d’information particulière et nous allons donc réduire le volume en convertissant l’image en niveaux de gris (un peu comme les films anciens, appelés d’ailleurs à tort en "noir et blanc", puisqu’ils sont en réalité en niveaux de gris). Chaque pixel n’aura donc plus besoin que d’un seul octet au lieu de 3 précédemment. Voici le résultat obtenu :

On peut noter que la teinte rosée a disparu mais que nous n’avons rien perdu quant à la netteté des détails.

Gommage des défauts

Toute image réelle a des défauts, qui se traduisent par du bruit pouvant perturber les traitements futurs. Nous allons donc chercher à les réduire en appliquant un flou à l’image :

Cela peut paraître paradoxal, car une telle opération fait intuitivement penser à une perte de qualité. Dans notre cas de figure cela constitue en réalité un avantage car les petits défauts disparaissent par cette opération, sans pour autant que la qualité globale ne s’en ressente beaucoup.

En termes mathématiques, le bruit est un signal de haute fréquence et le flou est équivalent à un filtre passe-bas. Un tel filtre laisse passer majoritairement les fréquences basses (d’où son nom) et atténue de ce fait le niveau du bruit.

Seuillage

Pour repérer la position des symboles nous allons procéder par silhouettage, qu’on appelle la détection de contours dans le monde du traitement d’image.

Il existe un grand nombre d’algorithmes possibles, dont les performances sont liées au type de l’image traitée. Dans notre cas de figure d’une image en niveaux de gris, l’une d’entre elles est de commencer par la simplifier en la convertissant en monochrome, c’est à dire ou chaque pixel sera noir ou blanc, sans aucune nuance intermédiaire. Cette opération porte le nom de seuillage, car elle consiste à affecter à un point la couleur noir ou blanc selon que son niveau de gris est en-dessous ou au-dessus d’un certain seuil. En général, ce seuil est déterminé selon l’étendue des valeurs rencontrées sur toute l’image (moyenne ou médiane par exemple). Cette transformation optimise énormément la détection de contour car le test d’appartenance à l’une des deux zones est très rapide (on compare une information codée sur un seul bit au lieu d’un octet complet).

En voici le résultat :

On constate que les paramètres utilisés ici ont transformé l’image en négatif. C’est par commodité du fait des conventions utilisée par les algorithmes proposés par OpenCV, mais cela ne change rien au principe.

Détection des contours

L’image ainsi simplifiée est ensuite soumise à un des opérateurs de détection de contours proposés par OpenCV, qui va nous retourner les poly-lignes (lignes composées d’une suite de segments connectés à la queue-leu-leu) représentant les contours.

Les résultats ont été superposés sur l’image d’origine pour mieux les illustrer :

On note deux types de tracé :

• les lignes jaunes représentant les poly-lignes, qui suivent assez fidèlement la délimitation entre les couleurs,
• les lignes bleues, qui matérialisent ce qu’on appelle les rectangles englobants (bounding boxes en Anglais) également retournés par OpenCV et qui sont les plus petits rectangles dont les côtés sont parallèles aux axes et qui contiennent intégralement le contour associé

L’intérêt de ces bounding boxes est de délimiter les zones d’intérêt de l’image, sur lesquelles vont porter les analyses à venir.

Rappelons-nous que nous cherchons pour le moment à repérer les quatre repères formés par des points noirs, afin de savoir où se trouve la grille des symboles et quelle en est la déformation.

Comme évoqué en début d’article, la technique utilisée va consister à répéter pour chaque bounding box les opérations suivantes :

• déformer l’image théorique du point (le dernier des symboles dans la palette montrée plus haut dans l’article) de telle manière qu’elle s’inscrive exactement dans la bounding box analysée
• pour chaque pixel de la portion d’image monochrome analysée contenue dans la bounding box, tester si sa couleur est identique à celle du pixel de l’image théorique situé à la même position
• calculer le pourcentage de correspondance sur l’ensemble de l’image du motif
• si ce pourcentage dépasse un certain seuil (par exemple 90%) on considère que le point a été reconnu

Cela va aboutir au résultat suivant, dans lequel seuls les contours des 4 points ont été retenus selon ces critères. Ils ont été retracés en vert tandis que tous les autres ont été supprimés :

Redressement et recadrage

Maintenant que nous avons la position des 4 bounding boxes des repères, et connaissant la distance entre les points du plateau et la grille-programme, nous utilisons les coordonnées de leurs centres respectifs pour calculer la transformation géométrique à appliquer à l’image de manière à :

• supprimer sa déformation (shear)
• la découper (cropping) afin de ne conserver que la zone rectangulaire dans laquelle sont disposées les cartes de programmation du robot

En voici le résultat :

A noter que cette transformation est appliquée à l’image en niveau de gris et non pas à celle en noir et blanc car c’est d’elle que nous allons repartir afin de ne pas risquer d’introduire des défauts (aka artefacts) en transformant géométriquement l’image monochrome. De telles défauts sont la conséquence de son absence de nuance entre le noir et le blanc.

Et on recommence

Nous allons appliquer à nouveau la même séquence d’opérations que précédemment, mais cette fois-ci en cherchant à reconnaître les différentes symboles utilisés sur les cartes.

Le plateau de programmation ayant été recadré, nous pouvons maintenant le subdiviser de manière à correspondre à sa grille 4x5 et à ne tenir compte que des contours positionnés au voisinage du centre des cases. Des ombres ou reflets dans l’image peuvent en effet générer des contours parasites.

En voici la succession de résultats intermédiaires :

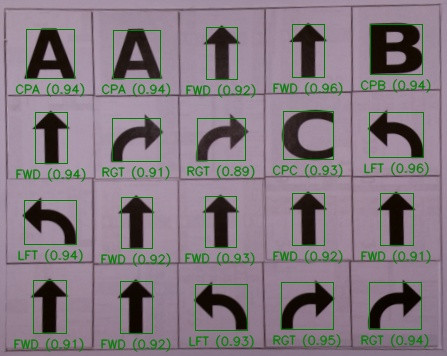
La dernière image indique pour chaque symbole reconnu le taux de correspondance mesuré. Du fait des similitudes et de la fluctuation des conditions d’éclairage, il est possible que différents symboles donnent un taux de correspondance supérieur au seuil de détection. Dans ce cas, n’est retenu que celui avec le taux le plus élevé.

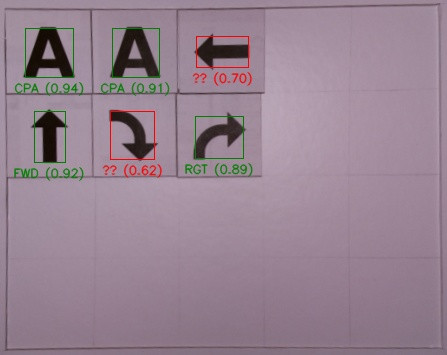
A titre d’exemple, l’image suivante montre des cas de symboles non reconnus (en rouge) :

Les résultats

Bien que relativement simple, la technique d’analyse utilisée s’est révélée très robuste à l’usage.

Le seul cas où elle ait été prise en défaut en détectant un faux positif est celui où la flèche rectiligne a été placée la tête en bas. La nature de la figure fait que le taux de correspondance a dépassé le seuil des 90% et qu’il a été le plus élevé de tous les symboles. L’image a donc été identifiée à tort comme un symbole correct.

Plusieurs parades sont possibles, la plus simple étant d’augmenter le seuil de reconnaissance à, par exemple, 92%. Cela présente cependant le risque de rendre le système moins tolérant à des variations liées aux conditions lumineuses ambiantes en générant ainsi plus de faux négatifs.

Une autre approche, à priori plus fiable, est de chercher à reconnaître aussi des correspondances avec des faux positifs possibles (la flèche à l’envers par exemple), dont on sait qu’ils donnent des résultats proches des vrais positifs. Elles donneront un résultat obligatoirement supérieur à ceux des vrais positifs, puisque plus de pixels correspondront, ce qui nous permettra de reconnaître qu’il s’agit alors d’un cas d’erreur et que le symbole est donc invalide. Si vous n’avez pas compris, relisez la phrase plus lentement et ça va faire tilt 😉

On pourrait dans l’absolu généraliser le principe en testant systématiquement les 4 orientations possibles de tous les symboles. Mais cela conduirait à quadrupler le temps total de traitement, sans réel bénéfice du fait de l’absence d’autres similitudes aussi marquées que celle présentée par notre flèche à l’envers.

La modification imaginée ici fera l’objet d’une mise à jour de l’application, et également de cet article pour en relater les résultats obtenus.

Conclusion

La chaîne de traitement utilisée pour TaxiBot est un bon exemple de compromis visant à obtenir un traitement le plus rapide possible tout en garantissant une fiabilité conforme aux attentes.

Les simplifications qui ont été faites se sont basées sur la connaissance à priori des éléments à reconnaître et des caractéristiques des images traitées. Cette démarche est très fréquemment utilisée et constitue ce qu’on appelle une optimisation de la complexité, dont l’objectif est de trouver le bon équilibre entre vitesse et/ou coût de traitement et fiabilité des résultats.

C’est une des démarches fondamentales du métier de l’ingénieur, dont un des rôles est de résoudre des problèmes complexes avec des solutions présentant le meilleur compromis résultat versus coût en fonction des contraintes du contexte.